正弦函数的图像与性质

正弦函数是数学中重要的三角函数之一，它描述了一个角的弧度与其正弦值之间的关系。正弦函数的图像表现为周期性的波动曲线，其性质包括振幅、周期、奇偶性等。正弦函数在数学、物理等领域有广泛的应用和重要性。

正弦函数的基本特征

正弦函数 \( y = \sin(x) \) 的图像以原点为中心对称，周期为 \( 2\pi \)，振幅为1。在每个周期内，正弦函数从0开始上升到1，然后下降到-1，再回到0。这种周期性变化使得正弦函数在描述周期性现象时非常有用。

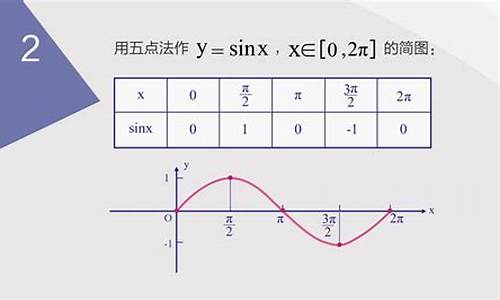
正弦函数的应用领域

正弦函数在物理学中用来描述波动、振动等现象，例如声波、光波的传播规律。在工程学中，正弦函数常用于分析交流电路的电压和电流变化。此外，正弦函数还在计算机图形学、信号处理等领域有着重要应用，如音频信号的处理和图像处理算法中的应用。

余弦函数的图像与性质

余弦函数 \( y = \cos(x) \) 也是一种周期性的波动函数，与正弦函数类似，但其相位不同。余弦函数的图像同样以原点为中心对称，周期为 \( 2\pi \)，振幅也为1。它与正弦函数的主要区别在于相位，即在 \( x = 0 \) 处达到最大值1。

余弦函数的特点与应用

余弦函数在数学建模和物理现象中常用来描述随时间或空间变化的周期性现象，例如天体运动、机械振动等。在工程学和自然科学中，余弦函数的应用广泛，如建筑设计中的结构分析、天体物理学中的星体运动预测等都需要用到余弦函数进行精确描述和计算。

总结

正弦函数和余弦函数作为重要的三角函数，在数学和应用领域都有着深远的影响。它们的周期性图像和数学性质不仅有助于理解数学规律，还在物理学、工程学和计算机科学等实际应用中发挥着重要作用。通过深入理解正弦函数和余弦函数的性质及其应用，可以更好地应对各种复杂的实际问题和挑战。